TestWorks/Coverage for Windows: TCAT C/C++ and TCAT/Java APG Metric Feature

Summary

APG (All Paths Generator) is a new addition to the capabilities of TCAT C/C++ and TCAT/Java.

You can now use the proprietary APG utility to calculate very-accurate execution path-class complexities of your C/C++ or Java program. This information will help you determine the relative complexity of functions/modules/objects so that you can focus your testing efforts on the most-complex functions/modules/objects.

APG Concepts Introduced

Any computer program contains the following three elements: nodes, edges and paths. A node is a branching point within a program. A node is represented by, for example, an if or case statement. The code that is contained between two nodes is called an edge. (For completeness sometimes a program graph is shown with an edge that contains no statements. This is called an empty edge.)

A path is the physical route that the program follows during program execution. More explicitly, the path is the set of edges used to run from program start to program finish. The order of edges in a path is important, just as the order of execution of statements in a program is important.

TCAT's apg capability can automatically enumerate and analyze the paths within a program based on its logic structure. These results can be used to evaluate program complexity. A few theories have shown that the number of errors in a program has a high correlation with the total number of path classes. Additionally, the amount of errors in a program has a low correlation with the cyclomatic complexity.

Accessing the APG Outputs

You get APG data directly from the WinDigraph program by clicking on the icons provided (see below). APG produces two outputs based on the contents of the current digraph:

• A summary set of statistics that provides a detailed overview of the structural complexity of the module.

• A list of paths in a special notation that accounts for loops and other structural features of the program.

You access these new capabilities by simply clicking on the two icons on the toolbar in the WinDigraph program.

The icon gives you the Possible Path Classes.

The icon gives you the Path Statistics.

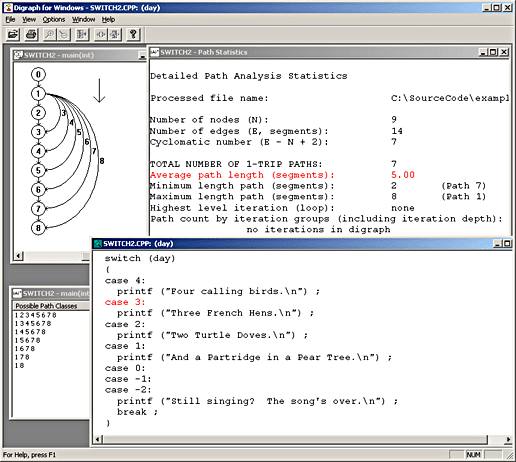
Here is a Screen Shot that shows the two new icons and also shows a sample program passage, the digraph TCAT produces for that program passage, and the outputs that APG produces.

Path Statistics

The Path Statistics icon gives you the Path Statistics. Here is a sample of the Path Statistics generated for the Sample Program shown below.

Detailed Path Analysis Statistics

Processed file name:   ElementTreePanel.dg

Number of nodes (N):   7
Number of edges (E, segments):  11
Cyclomatic number (E - N + 2):  6

TOTAL NUMBER OF 1-TRIP PATHS:  9
Average path length (segments):  6.22
Minimum length path (segments):  2 (Path 1)
Maximum length path (segments):  10 (Path 4)
Highest level iteration (loop):  1 (Path 5)

Path count by iteration groups (including iteration depth):
  BASIS PATHS (no iteration):  5
  Level 1 loop(s):  4
Stopped at 1 iteration groups

Basic Information: The number of Nodes (N) and the number of Edges (E, Segments) is taken from the structure of the program whose Processed [digraph] file name is given on the output.

The cyclomatic number E - N + 2 for this graph is shown next. The cyclomatic number is a measure of the static complexity of the program.

The Total Number of 1-Trip Paths in the program is given next. This number is calculated based on assuming that one starts at the entry node and proceeds through the program to an exit node [there could be several exit nodes], made on one visit to each edge along the way.

Advanced Information: The data given next provides detailed analysis of the actual set of paths generated by APG, including the Average Path Length (segments) and the longest and shortest path in the program. In addition, APG computes the Highest Level Iteration (Loop) for the program and tells you which path, in sequence, first exercises that loop.

Interpretation of Values: The statistics produced by APG give valuable insight on the likely complexity of testing of a given program, and may be used as an indicator of where best to aim limited testing and analysis effort.

The Total Number of 1-Trip Paths is a measure of the potential dynamic complexity of the program.

Note: Some simple programs with low cyclomatic complexity can have high dynamic complexity, and some program with very high cyclomatic complexity can, in fact, have relatively low dynamic complexity. It all depends on the program, of course, but other things being equal the total path count is the more reliable of the two complexity indicators at indicating testing difficulty.

Path Class Enumeration

The Path Class icon gives you the Possible Path Classes. Here is a sample of the Path Classes generated for the Sample Program shown below.

 1 2
 1 3 4 6 8 <{ 6 8 9 }> 7 10
 1 3 4 6 8 <{ 6 8 9 }> 7 11
 1 3 4 6 9 <{ 6 8 9 }> 7 10
 1 3 4 6 9 <{ 6 8 9 }> 7 11
 1 3 4 7 10
 1 3 4 7 11
 1 3 5 10
 1 3 5 11

In this display each line represents one 1-trip path through the program. the sequence of edges is important; it indicates the order of segment execution.

Loops are indicated using either the <{ edges }> or the [{ edges }] notation. When you see this structure you should read it as implying that there will be a repetition of edges. How many times the sequence is repeated is not specified; each "loop" is grouped into that particular path class. There are two types of possible groupings:

The <{ edges }> notation means that there will be zero or more repetitions of edge sequences involving the edges enumerated in within the { edges } list.

The [{ edges }] notation means that there will be one or more repetitions of edge sequences involving the edges enumerated in within the { edges } list.

Simple IF Statement Example

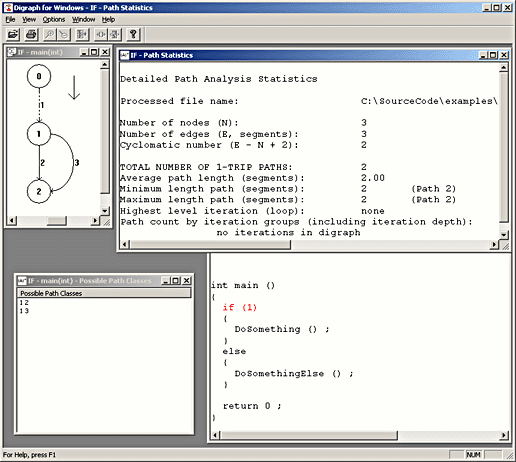
The screen shot below shows the behavior of APG when presented with a program that contains a single if statement.

Simple WHILE Statement Example

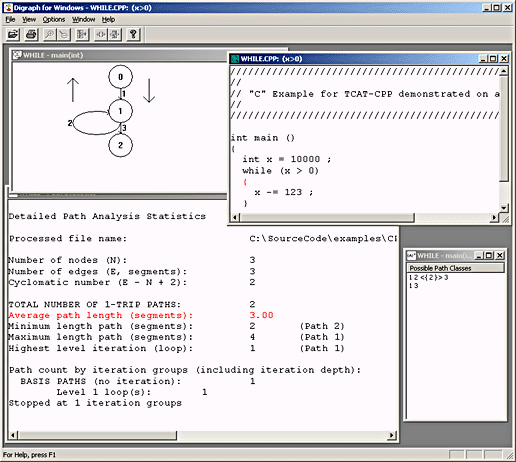
The screen shot below shows the behavior of APG when presented with a program that contains a single while statement.

Simple WHILE with IF Example

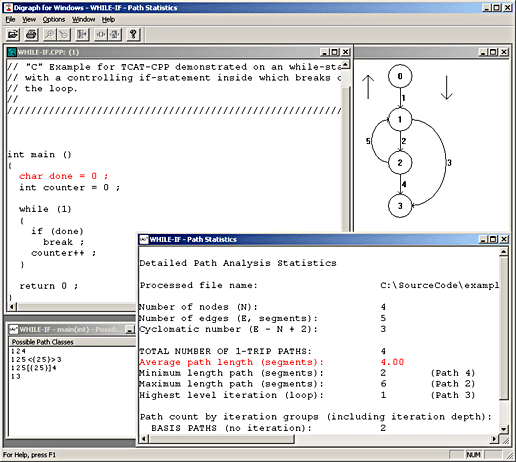
The screen shot below shows the behavior of APG when presented with a program that contains a single while statement that contains an if statement.

Note that the cyclomatic complexity is 3 but that the actual path count is 4. This difference is accounted for by the fact that, in pure-mathematical terms, the cycle in the program is not single-entry/single-exit as would be required in pure structured programs, in which the path-class count is predicted by the cyclomatic complexity. This construction is very common in actual programs; the difference between the path count and the cyclomatic complexity is discussed in more detail below.

Simple CASE Statement with Breaks Example

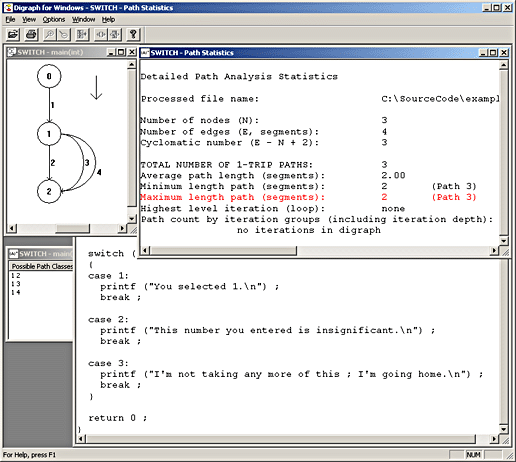
The screen shot below shows the behavior of APG when presented with a program that contains a single case statement in which each case alternative is followed by a break.

Simple CASE Statement with No Breaks Example

The screen shot below shows the behavior of APG when presented with a program that contains a single case statement in which each case alternative is not followed by a break. This form of a case causes additional complexity because the flow of control "drops through" each case in the sequence.

Sample Program With Iteration Example

This program shows a little more complex situation, one that involves some logical branching and some looping. Note in this case there are several non-iterative paths and several looping [iterative] paths.

About APG's Internal Operation

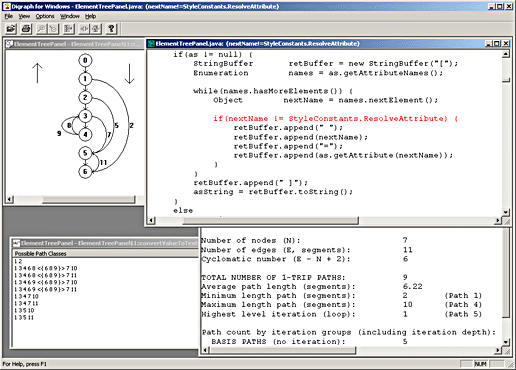
APG is a TCAT utility that examines program digraphs produced by the TCAT instrumenter using the data from the current WinDigraph display. It generates equivalence classes of program flows based on the structure of this digraph. APG uses a recursive descent analysis of the digraph that employs a proprietary search pruning capability to permit generating program flows into actual equivalence classes.

APG generated equivalence classes that have the property that, disregarding repetition counts on edges within loops (and loops within loops, and loops within loops within loops, etc.) any actual program execution sequence will always resolve to exactly one of the identified equivalence classes.

Because the equivalence classes are generated based on structural characteristics alone it is possible that the class set can contain sequences that are structurally feasible but which are not logically feasible. In other words, the equivalence classes generated are always a superset of the set of possible realizable program execution sequences.